ベンフォードの法則

ベンフォードの法則とは

ベンフォードの法則（Benford’s law）とは、現実世界に現れる多くの数値データでは、先頭の数字が「1」になる確率が最も高く、数字が大きくなるほどその確率が下がっていくという不思議な法則です。

金額を表すもの、重さや距離を表すもの。選挙の投票数のようにその量を示すもの。

などなど、世の中にはいろんな数字が存在します。

実は、その数字の先頭桁の数字は１～９まで均等に存在するのではなく、特定の偏りになるというものです。

　

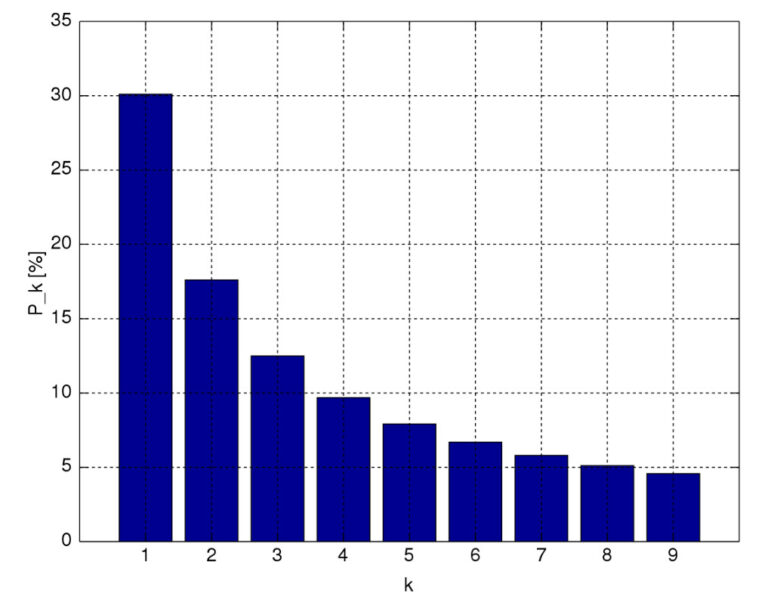
具体的には、数値の一桁目が

　
という偏りを示します。

　

この法則は、1938年にアメリカの物理学者 フランク・ベンフォード によって体系的に示されました。

ただし、発見自体はそれ以前からあり、1881年には天文学者サイモン・ニューコムが「対数表の最初のページほど汚れている」という観察を報告しています。

直感的には「1〜9は同じ確率で出そう」と思いがちですが、実際の社会データはそうなっていません。

ここに、ベンフォードの法則の面白さがあります。

　

　

世の中の数字、最初の1桁だいたい「１」説

この法則が成り立つ理由は、「数が成長する過程」にあります。

例えば、売上、人口、資産、フォロワー数などは、

1 → 2 → 3 → …

と線形に増えるのではなく、倍率的に増えていくことが多いです。

数は

1台 → 2台 → 4台 → 8台 → 16台 → 32台…

のように増えると、

「1」で始まる期間は長く、「9」で始まる期間は非常に短くなります。

　

この違いが、先頭の数字の出現頻度の差を生み出します。

重要なのは、この法則が

など、人為的に作られていない広範なデータで特によく当てはまる点です。

　

　

その数字は自然な数字か

ベンフォードの法則の最大のメリットは、「不自然な数字」を見抜けることです。

実際にこの法則は、

• 会計監査
• 不正会計の検出
• 税務調査
• 選挙データの分析

などに活用されています。

人が「それっぽく」数字を作ると、無意識に1〜9を均等に使ってしまいがちです。

その結果、ベンフォードの法則から大きく外れた分布になります。

日常生活でも、
「この数字、やけにキリが良すぎないか？」
「なぜか不自然に整っていないか？」
と疑問を持つ視点を与えてくれます。

ベンフォードの法則は、数字を信じ切る前に一歩立ち止まり、現実らしさを確かめるためのレンズとして使える考え方なのです。

（参考文献）
鈴木貴博「米大統領選は不正だらけ」根強い都市伝説を裏付ける奇妙な証拠　ダイヤモンドオンライン(2020)
Frank Benford . “The law of anomalous numbers”. Proceedings of the American Philosophical Societ（1938）